A Beautiful Geometric Approach at a Simple Problem
A trivial looking problem leads to a beautiful solution.
Written By: Andrew Wang, Asia Chapter Leader
Problem: Evaluate the next term in the sequence: 1/15, 1/23, 1/39, 1/63.
This problem looks easy at first, the number sequence 15 + 8 leads to 23, 23 + 16 leads to 39, 39 + 24 leads to 63, and so on. We are just adding multiples of 8 to the denominator. Therefore, the obvious answer should be, since 63 + 32 = 95, so 1/95, right?
Well, the answer is correct, but what if I told you that there is a much more beautiful solution than this?
In this case, we have to use a famous geometry pattern called the Pappus Chain.
The Pappus Chain, a Beautiful Geometric Diagram.
The Pappus Chain
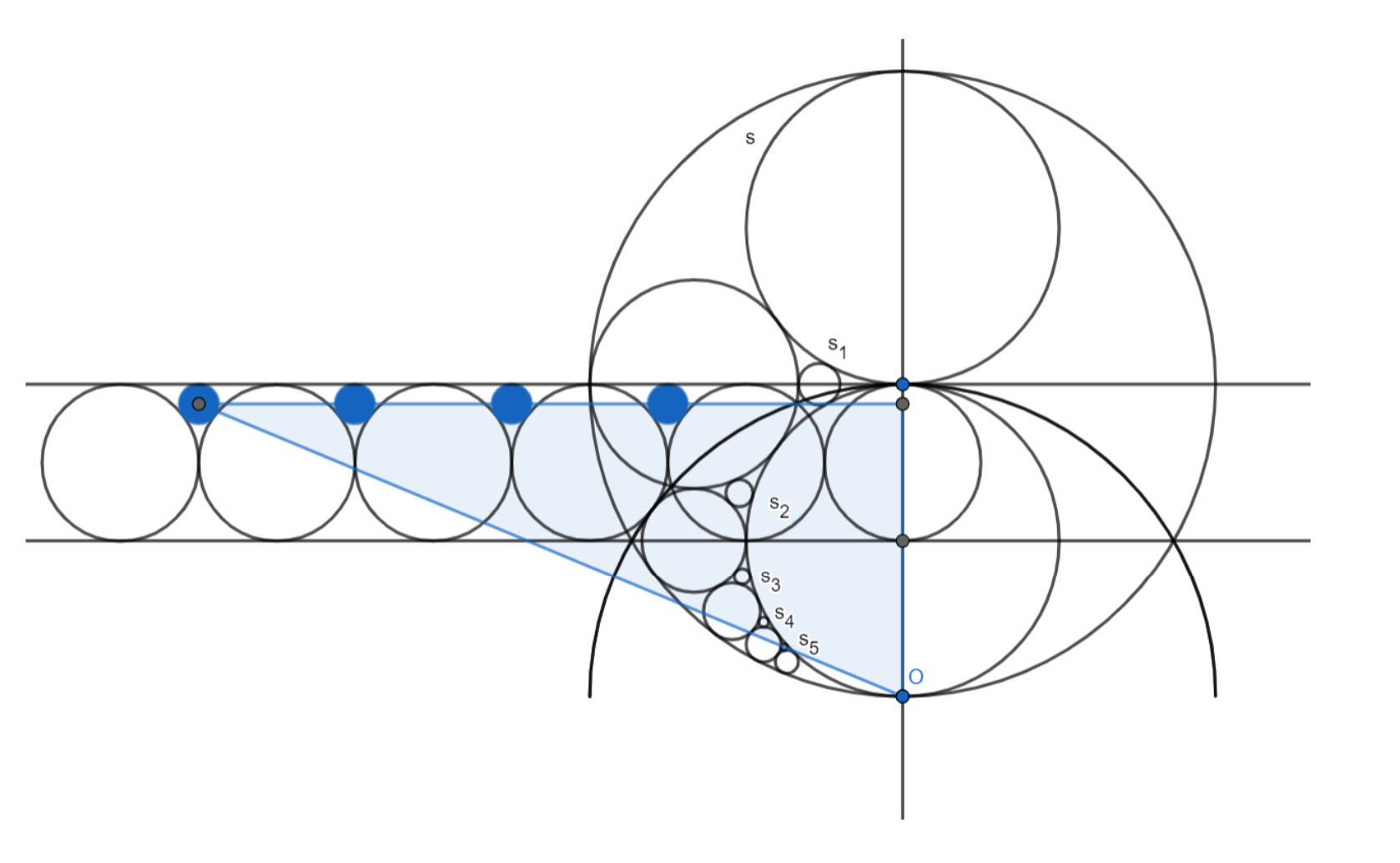
A Pappus Chain starts with a large circle. Let’s say it’s a circle S with radius R, with 2 other circles a1 and a2, each with radius 12R and touching the sides of the big circle, or being tangential to it. We can carry on doing this, with another circle a3 tangent to a1, a2, and S, circle a4 tangent to a1, a3 and S, and so on. Furthermore, we can construct a circle s₁ which is tangent to a1, a2, and a3, s₂ is tangent to a1, a2, and a4, and so on.
Now, for the sake of simplicity, it is already given that the radius of circle s₁, s₂, s₃ and s₄ is 115, 123, 139 and 163 of the circle S respectively. So then the rephrased question is: what is the ratio of the radius of circle s₅ to that of circle S?
Seeing this, we would naturally want to just use a ruler to measure the radius of circle s₅ and calculate its ratio. However, the circle s₅ is so small that it would be nearly impossible to measure its radius accurately! In addition, these circles are in a pattern called the Pappus Chain, how could we reliably find out the ratio of the radius of subsequent circles?
The best way is to use inversion. We can find and prove the ratio of the radius of circle s₅ with this method.
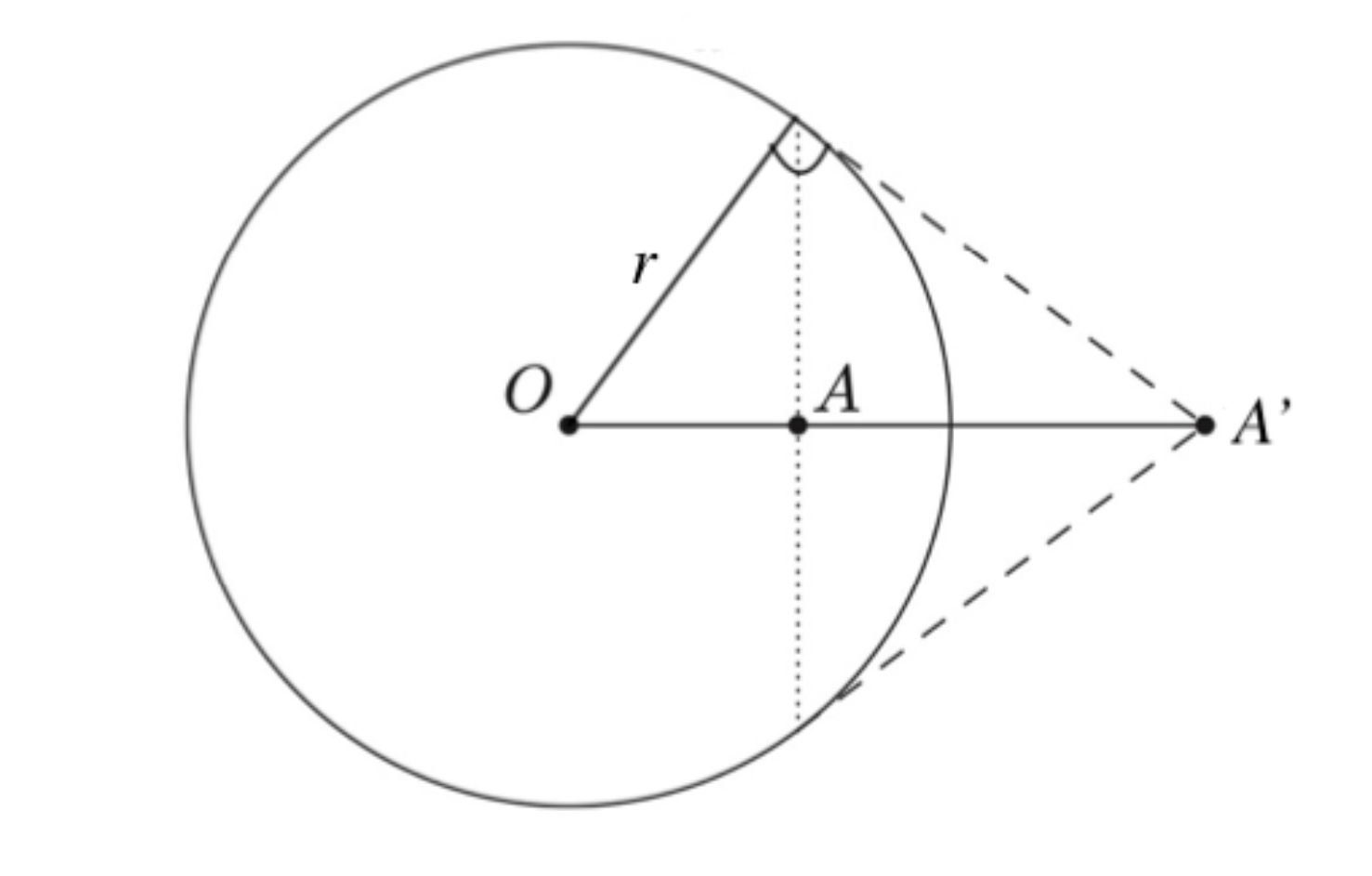
So, what is inversion? It is pretty hard-core, but it all boils down to the equation OA ⋅ OA’ = r2, where O and r is the center and radius of the circle of inversion respectively, A is the point being inverted, and A’ is the inverted point. We are just transforming point A to A’.
The Pappus Chain, Inverted
Refer to the diagram above. So, drawing a semicircle with the center at O, we then inverse the circle s and the circles in s about the semicircle and we get two parallel lines with 6 circles adjacent to one another. Then, the blue circles represent circles s₁, s2, s3, s4 and s5 when inverted.
We let the radius of circle S be R. By drawing a right-angled triangle touching the center of circle s5’, A, we can find out the length of the base of the triangle as 1516R and the height as 92R. Then, using Pythagoras’ Theorem, we calculate the hypotenuse of the triangle to be 3916R.
We let point C be the point where the hypotenuse of the triangle reaches the end of the blue circle and point B be the point where the hypotenuse of the triangle reaches the start of the blue circle. As such, we can find the length of OC to be 3916R + 116R = 4016R. The length of OB would then be 3916R- 116R = 3816R. By inverting OB and OC, we can find the diameter of the circle s5 which is 819R-820R=295R. Lastly, we divide the result by 2 to get the radius of the circle s5 in relation to R which is 295R ÷ 2 = 195R, and we are done.
Wrapping Up
Although this solution does seem a bit overkill, its usage of the Pappus Chain and Inversion goes to show how magnificent geometry is. If you found inversion interesting, do leave a comment below the blog, and we will answer any queries you have about it. Trust me, you will never look at circles the same way again.